
Энергия магнитного поля и её формула: как рассчитывается
Магнитное поле — это особый вид материи, который создаётся при помощи движущихся электрических зарядов, т.е. электрического тока. Оно обладает не только способностью воздействовать на другие токи или магнитные тела, но и запасает в себе энергию. В этой теме подробно рассмотрим, из чего складывается энергия магнитного поля, как она рассчитывается и в каких сферах применяется.
Что такое энергия магнитного поля
Энергия магнитного поля — это та энергия, которая накапливается в пространстве, где существует магнитное поле. Она не появляется из ниоткуда: её создаёт ток, протекающий по проводнику, а именно — катушке индуктивности. Если мы подключим катушку к источнику тока, часть энергии этого источника будет тратится на то, чтобы «разогнать» магнитное поле вокруг витков провода.
Важно понимать, что магнитное поле — часть электромагнитного поля, и его связана с общей энергией этого взаимодействия
Пример с катушкой индуктивности
Самые очевидные проявления энергии магнитного поля можно рассмотреть на примере катушек. Сама по себе катушка — это провод, скрученный в витки. Чем больше витков и чем плотнее они расположены, тем сильнее магнитное поле внутри. Катушка имеет свой параметр — индуктивность, который обозначается буквой L и измеряется в генри (Гн). Чем больше индуктивность, тем больше энергии способна запасти катушка.
Формула энергии магнитного поля
Энергия магнитного поля обозначается буквой W и рассчитывается по формуле:
 где:
где:
W — энергия магнитного поля (в джоулях, Дж);
L — индуктивность катушки (в генри, Гн);
I — сила тока катушки индуктивности (в амперах, А).
Эта формула говорит нам о том, что:
энергия пропорциональна индуктивности: чем больше L, тем больше запасается энергии;
энергия пропорциональна квадрату тока: если удвоить ток, энергия увеличится в четыре раза.
Примеры расчётов
Представим два простых примера:
Катушка с индуктивностью 0,2 Гн и током 10 А:
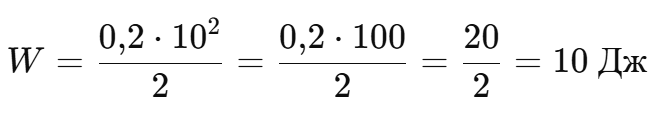
Катушка с индуктивностью 0,5 Гн и током 2 А:
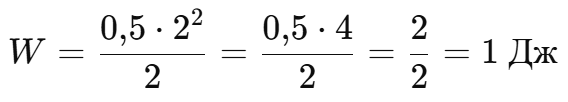
Как можно понять из вышеуказанных расчетов, даже при сравнительно небольшом токе и индуктивности, есть возможность накопить некоторое количество энергии.
Где используется энергия магнитного поля
Знания об энергии магнитного поля широко применяется в электротехнике и радиоэлектронике. Катушки индуктивности и соленоиды применяются в:
трансформаторах;
двигателях;
генераторах;
электронных фильтрах и колебательных контурах.
Например, в трансформаторе катушки создают и передают магнитное поле, которое в свою очередь пропускает энергию между цепями. В электродвигателе энергия магнитного поля превращается в механическую работу.
Также необходимо учитывать, что при отключении тока в катушке магнитное поле разрушается, и энергия возвращается обратно — она может выделиться в виде тока самоиндукции или тепла. Поэтому в практических схемах применяются специальные компоненты, которые предотвращают скачки тока при разрыве цепи.
Связь с другими видами энергии
Интересный факт: в физике энергия магнитного поля часто рассматривается вместе с энергией электрического поля. Например, в колебательном контуре происходит постоянный переход энергии из электрической формы в магнитную и обратно. Этот принцип лежит в основе работы радиопередатчиков и других устройств, использующих колебания тока.
Так, энергия магнитного поля напрямую связана с тем, как работает катушка индуктивности, как изменяется ток катушки индуктивности, и какова сила тока в проводнике. В физике также рассматривается понятие сила магнитного тока, которое помогает глубже понять процессы в электрических цепях.
Это важное физическое явление, которое показывает, как ток может создавать и накапливать энергию вокруг себя. Зная простую формулу, можно легко рассчитать количество энергии, запасённой в катушке.
Вывод
Эта тема не только важна для понимания основ физики, но и напрямую связана с реальными приборами, которыми мы пользуемся каждый день. Понимание процессов, происходящих в магнитном поле, это ключ к развитию новых технологий и устройств будущего.
Обложка и иллюстрации сгенерированы ИИ: labs.google/fx/tools/whisk























Комментарии